RADICACIÓN DE ENTEROS.
La radicación es la operación que “deshace” la potenciación.
En el ejemplo anterior, el 9 se llama radicando, el 2 índice y el resultado 3, raíz.
La definición formal de esta operación es la siguiente:
Si n es un número natural, se dice que el número entero a es la raíz enésima del número entero b, si b es la potencia enésima de a. Es decir:
Veamos otros ejemplos:
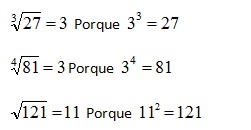
Veamos que sucede cuando el radicando es un número negativo:
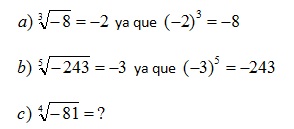
En el ultimo ejemplo se debería buscar un número elevado "a la cuatro" que de como resultado -81, ¿existirá algún número que cumpla esa condición?
Si recordaste lo estudiado cuando se trabajó con la operación de potenciación, tu respuesta debería ser negativa, no existe ningún número entero que cumpla esa condición.
En general: cuando el índice e par y el radicando un número negativo, el resultado no existe en el conjunto de los números enteros.
Algunas reglas en la radicación de números enteros
Trabajaremos muy poco las raíces con números enteros. Solamente señalar alguna novedad respecto a las raíces de números naturales.
1.- La primera es observar que las raíces cuadradas de los números positivos tienen dos soluciones: La positiva y la negativa:  Pero también:  Porque (− 8)2 = (− 8) ⋅ (− 8) = 64 Esta doble solución de la raíz cuadrada se suele representar así:  2.- Las raíces cuadradas de los números negativos no tienen solución. O, más exactamente, no tienen solución en el campo numérico de los enteros.  3.- La raíz cúbica de un número positivo tiene solución positiva:  4.- La raíz cúbica de un número negativo tiene solución negativa: |
No hay comentarios.:
Publicar un comentario
Participa en este blog con tu cuenta Google (gmail). Debes elaborar una pregunta relacionada con el tema (hasta 10 puntos) o responder alguna elaborada por tus compañeros (hasta 5 puntos). El puntaje se asigna por orden de llegada.