QUÉ ES LA GEOMETRÍA EUCLIDIANA?
DEFINICIÓN DE GEOMETRÍA
Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos,politopos (que incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.).Es la base teórica de la geometría descriptiva o del dibujo técnico. También da fundamento a instrumentos como el compás, el teodolito, el pantógrafo o el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales).
Sus orígenes se remontan a la solución de problemas concretos relativos a medidas. Tiene su aplicación práctica en física aplicada,mecánica, arquitectura, geografía, cartografía, astronomía, náutica, topografía, balística, etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanía.
Segmentos congruentes
Dos segmentos son congruentes cuando superpuestos coinciden en todos sus puntos. Para ello basta con mostrar que coinciden en sus extremos.
Es decir que si por algún tipo de desplazamiento o movimiento pudiésemos poner un segmento sobre otro, todos sus puntos coincidirían.
Los segmentos a y b son congruentes, si desplazamos el segmento b sobre el a y hacemos coincidir el punto Ccon el punto A, también podemos hacer coincidir los puntos B y D.
Cuando dos segmentos son congruentes se dicen que tienen la misma longitud.
Ángulos congruentes
Dos ángulos congruentes miden lo mismo en grados. Así de fácil.
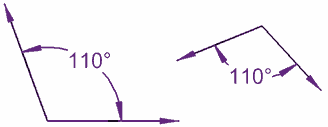
Estos ángulos son congruentes.
No tienen que apuntar en la misma dirección.
No tienen por qué estar entre líneas del mismo tamaño.
| Congruentes - ¿por qué usamos una palabreja que en realidad significa "iguales"? Probablemente porque sólo serían "iguales" si uno está superpuesto al otro. La palabra viene de latín congruere, que significa más o menos "estar de acuerdo". NÚMEROS RACIONALES "Q" |
Los números racionales, son el conjunto de números fraccionarios y números enteros representados por medio de fracciones.
Este conjunto está situado en la recta real numérica pero a diferencia de los números naturales que son consecutivos, por ejemplo a 4 le sigue 5 y a este a su vez le sigue el 6, y los números negativos cuya consecución se da así, a -9 le sigue -8 y a este a su vez le sigue -7.
Los números racionales no poseen consecución pues entre cada número racional existen infinitos números que solo podrían ser escritos durante toda la eternidad.
Este conjunto está situado en la recta real numérica pero a diferencia de los números naturales que son consecutivos, por ejemplo a 4 le sigue 5 y a este a su vez le sigue el 6, y los números negativos cuya consecución se da así, a -9 le sigue -8 y a este a su vez le sigue -7.
Los números racionales no poseen consecución pues entre cada número racional existen infinitos números que solo podrían ser escritos durante toda la eternidad.
Todos los números fraccionarios son números racionales, y sirven para representar medidas.
Definición de números racionales
Es el cociente de dos números enteros o más precisamente, un número entero y un número natural positivo. Es decir que es un número racional, es un número que se escribe mediante una fracción.
Los números racionales son números fraccionarios, sin embargo los números enteros también pueden ser expresados como fracción, por lo tanto también pueden ser tomados como números racionales con el simple hecho de dar un cociente entre el número entero y el número 1 como denominador.
Al conjunto de los números racionales se lo denota con la letra ℚ, que viene de la palabra anglosajona “Quotient” traducción literal de cociente.
Un número racional puede ser expresado de diferentes maneras, sin alterar su cantidad mediante fracciones equivalentes, por ejemplo:
½ puede ser expresado como 2/4 o 4/8, debido a que estas son fracciones reducibles.
Dependiendo de su expresión decimal, estos son:
Los números racionales exactos: cuya representación decimal tiene un número determinado y fijo de cifras, por ejemplo:
1/8 es igual a 0,125.
Los números racionales periódicos: de los cuales sus decimales tienen un número ilimitado de cifras.
Se dividen en dos:
a) Periódicos puros: La cifra que se repite se encuentra inmediatamente después de la coma, por ejemplo 0,6363636363…
b) Periódicos mixtos: La cifra que se repite está después de un número determinado de cifras, por ejemplo 5,48176363636363…
a) Periódicos puros: La cifra que se repite se encuentra inmediatamente después de la coma, por ejemplo 0,6363636363…
b) Periódicos mixtos: La cifra que se repite está después de un número determinado de cifras, por ejemplo 5,48176363636363…
Algunos temas a estudiar en geometría
Qué es la Geometría Plana o Euclidiana
Definiciones: Punto, recta, semirrecta, ángulo, plano, puntos coplanares y semiplano
Congruencia de segmentos: reflexividad, simetría, transitividad y punto medio.
Congruencia de ángulos: reflexividad, simetría, transitividad y bisectríz.
Clasificación de ángulos según su medida, posición y suma.
Triángulos y su clasificación según sus lados y sus ángulo.
Altura, mediana, bisectriz y mediatriz de un triángulo.
Congruencia de triángulos y el criterio Lado - Ángulo - Lado (LAL)
Congruencia de triángulos y el criterio Ángulo - Lado - Ángulo (ALA).
Congruencia de triángulos y el criterio Lado - Lado - Lado (LLL)
Definición y propiedades de rectas perpendiculares y paralelas.
Ángulos alternos internos entre paralelas.
Ángulos correspondientes entre paralelas.
Ángulos consecutivos internos entre paralelas.
Baricentro y las medianas de un triángulo.
Incentro y las bisectrices de un triángulo.
Polígonos y Cuadriláteros: cuadrado, rectángulo, paralelogramo, rombo y trapecio.
Paralelogramos y propiedades: congruencia de lados opuestos y suma de ángulos internos.
Paralelogramos y propiedades: ángulos opuestos congruentes. Parte 2.
Paralelogramos y propiedades: lados congruentes, paralelos y diagonales. Parte 3.
Cuadrados, rectángulos y sus propiedades: diagonales, perpendiculares y bisectrices.
Rombos y sus propiedades: diagonales, perpendiculares y bisectrices.
Trapecio isósceles: los ángulos adyacentes de la base son congruentes.
La circunferencia, arcos de circunferencia y el ángulo central.
Circunferencia.
Demostración del teorema de Thales
vi los vídeos y estuvieron muy bien explicados
ResponderBorrar